By Cadence
本文要點
有限元素分析 (FEA) 是在複雜幾何中為微分方程求解的一種基本的數值計算方法。 |
|
這些複雜的系統可能無法人工求解,而且可能存在不同物理現象之間的耦合,特別是在電子領域。 |
|
頂尖的有限元系統將直接從 PCB Layout 中獲取資料,並使用標準的數值演算法創建多物理場模擬。 |
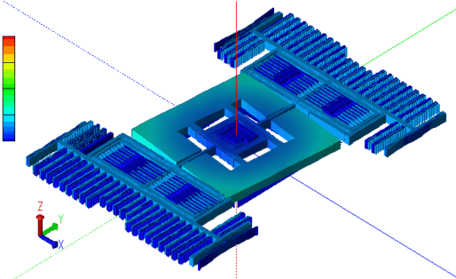
有限元建模為複雜的電子系統提供了直觀的多物理場模擬結果。
微分方程是用來描述物理現象的主要數學工具。從牛頓定律到薛定諤方程 (Schrodinger equation),任何物理系統都有一個可控制其行為的微分方程。常微分方程和偏微分方程求解是應用數學研究的一個長期課題,為此已開發出許多計算軟體。
高度精確的數值計算方法可以借助當今的現代計算能力來實現。以前,這些方法可能難以實現,而且容易出現巨大錯誤,但現在,人們可以使用常規電腦在合理的時間內完成這些數值計算。在檢查穩態系統時,有限元建模等方法的結果也非常準確。如果我們需要對複雜電子系統的行為進行建模,那麼使用有限元建模來檢查在穩態下發生的情況則是明智之舉。
什麼是有限元建模?
有限元建模 (Finite Element Modeling ,即 FEM) 涉及到一類使用反覆運算求解演算法來求解一系列離散微分方程的方法。在此類方法中,系統被分解並離散成小單元,並在空間的每一點上確定控制該系統的微分方程的解。
有限元建模的第一步是在系統的邊界內對控制相關現象的微分方程進行離散化處理。這涉及到在創建有限元建模模擬時,向數值求解器輸入一系列特定的資訊:
邊界條件 |
|
網格創建 |
|
初始條件 (用於及時反覆運算的問題) |
有限元建模的應用
相關的典型問題包括結構分析、熱量傳導 / 擴散、流體流動、品質傳遞和電磁勢 (靜態場和電壓分佈)。多物理場耦合問題只要在時間上是龐加萊穩定 (Poincare’ stable) 的,就可以加以處理。此外,非線性問題可以用特定的求解器常式來解決,從而可以處理 CFD 問題。

波導結構的有限元建模結果。
FEM 與 FVM
在對流體動力學問題進行建模時,有限體積法 (Finite Element Modeling ,即 FVM) 比有限元法更受常見。特別是在系統的控制微分方程使用非自伴隨微分運算元時,可以使用這種方法。該方法求解控制方程的積分形式,因此可以忽略有限元 / 有限差分方法中要求的局部連續性。
例如積分形式的麥克斯韋方程,可以寫成:
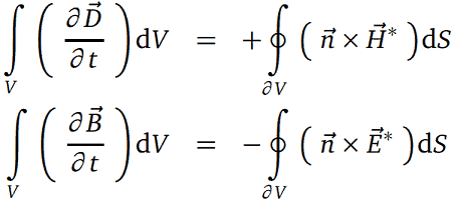
麥克斯韋方程 (Maxwell’s equations) 的積分形式。
這些方程包含在系統特定體積內計算的定積分,因此稱為「有限體積法」。FVM 只是將系統中的不同區域拼接在一起,拼接方式與有限元建模採取的方式相同,但網格是 3D 體而非一系列連接的點。
有限差分時域
這種數值建模方法通常用於時域問題,其中系統被直接離散化,也就是不使用基函數。實際上,系統中的任意點都可以用於將控制方程中的導數轉換為有限差分。
創建有限元模擬的技巧
在開始運行有限元模擬之前,我們可以採取一些簡單的步驟來簡化系統,並在不犧牲精度的情況下加快收斂速度。
識別對稱性和同質性 |
|
選定網格密度 |
|
確定靜態與動態係數 |
一旦我們將系統減少到更少的維度 (如果可能的話) 並確定了所需的網格密度,最好的場求解工具可以將 PCB 或 IC layout 轉換成網格模型,用於解決多物理場問題。一些功能強大的軟體工具可以實現有限元建模的網格自動生成。然後,我們可以選擇用於模擬的特定數值演算法,以達到所需的精度。
Clarity™ 3D Solver 軟體是 Cadence 公司智慧系統設計戰略下推出的第一款產品,其突破性的電磁場 (EM) 模擬技術可提供 10 倍的性能、無限容量,以及黃金標準的模擬精度。得益於最先進的分散式平行計算技術,Clarity 3D Solver 可有效解決在晶片、封裝、PCB、接外掛程式和電纜上設計複雜 3D 結構時遇到的電磁挑戰——為任何擁有桌面、高性能計算 (HPC) 或雲計算資源的工程師提供整體的 3D 分析。
譯文授權轉載出處 (映陽科技協同校閱)
長按識別 QRcode,關注「Cadence 楷登 PCB 及封裝資源中心」



